Caught Slippin'
I don't think I've truly appreciated the importance of the full slip curve in making cars feel... normal.
- Peak slip? Sure, that's the bit you're aiming for as a driver.
- Initial slope? Yeah, that's what every piece of vehicle analysis fixates on.
- The dropoff after peak? That's what every sim racer fixates on.
- The bit between initial slope and peak slip? Uhhhhhh...
In my driving physics attempts, I've been fighting with trying to make a car behave nicely. Nicely being a vague term that I'll know when I reach it, and I've given up trying to define more tightly because I'm learning that I understand less and less the longer I go on.
One of the big ticket items I've wanted in my driving model is a very simple to parameterise tyre slip curve. Ideally, I want the slip where the friction peak occurs, the magnitude of the peak, and then some way of tweaking the grip beyond that. More options would be nice, but I'd take elements that directly describe what they do rather than many interlinking components. ahemmagicformulaahem.
The upshot is I created this system to generate slip curves.
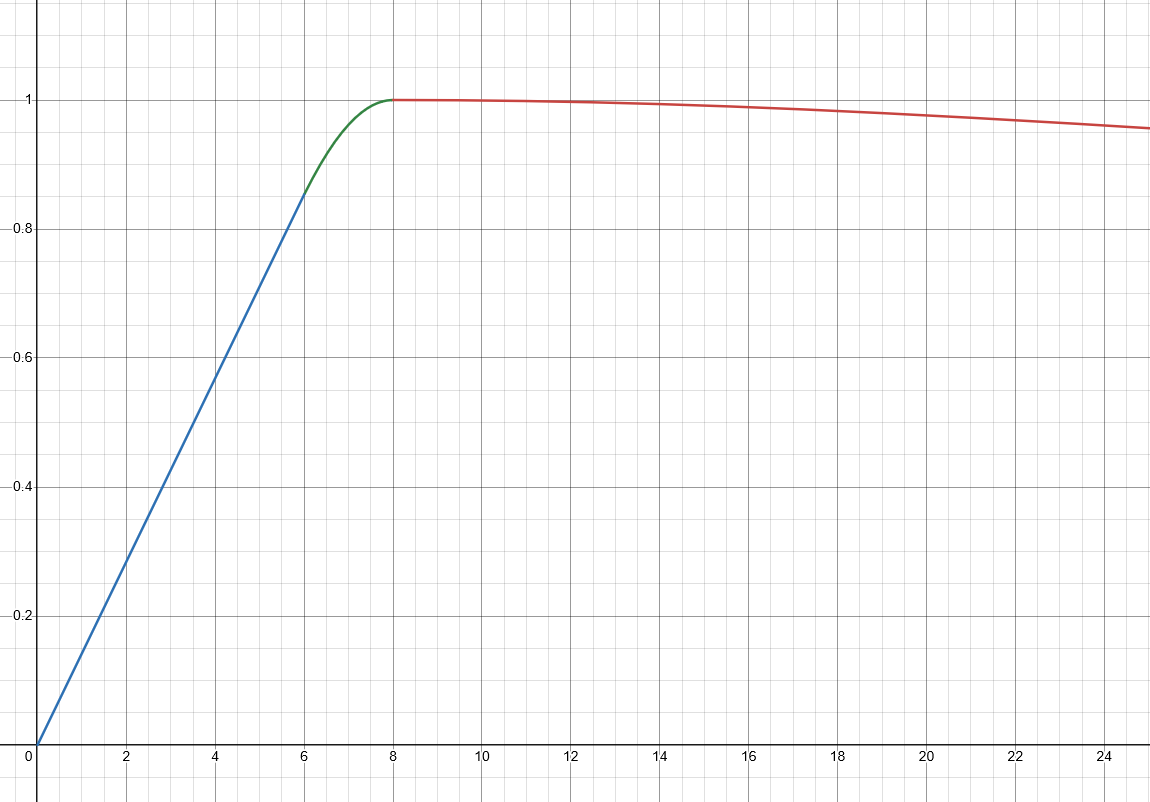
It's a simple enough system. It generates a linear region, joins it up to a curve, and then uses a cos function to generate a bit of a dropoff to some abitrary slip in the distance. On paper, it looks fine. It doesn't resemble any tyre data I've ever seen, but I figured the long linear section would be great for predictable driving and using all those equations in the automotive industry that assume tyres are totally linear. In reality, it's near useless for anything but driving at peak slip. Which is why I've been blinded by it for so long, when my main test course has been a bunch of tight, low speed corners with little to no opportunity for steering below peak lateral-g.
The fact that real tyres generate forces at a decaying rate as slip rises is, as it turns out, a feature, not a bug. I'm still figuring out quite how to express this though. I think it comes from the fact that with a constant rate of force vs slip, either your cornering stiffness is unnaturally high, so you don't get the yaw angle you'd naturally expect, or unnaturally low and so the car rotates rapidly because you've turned the wheel and the rear's lagging behind. But I dislike this psychological based explanation, I don't think it's so firmly tied to the expectations of how cars should behave. Plenty of arcade racers don't behave like real cars and yet drive fine. A predictable tyre appears to be one with quite a high peak slip angle, but a very steep initial curve so low lateral accelerations are reactive. So a quick flick of the wheel gives you enough to change lanes, but there's still a delay before you're attempting to put the car at the limit. When I match my system to a pacejka curve of the same initial cornering stiffness, the pacejka curve feels far less twitchy. In fact, have a visual comparison:
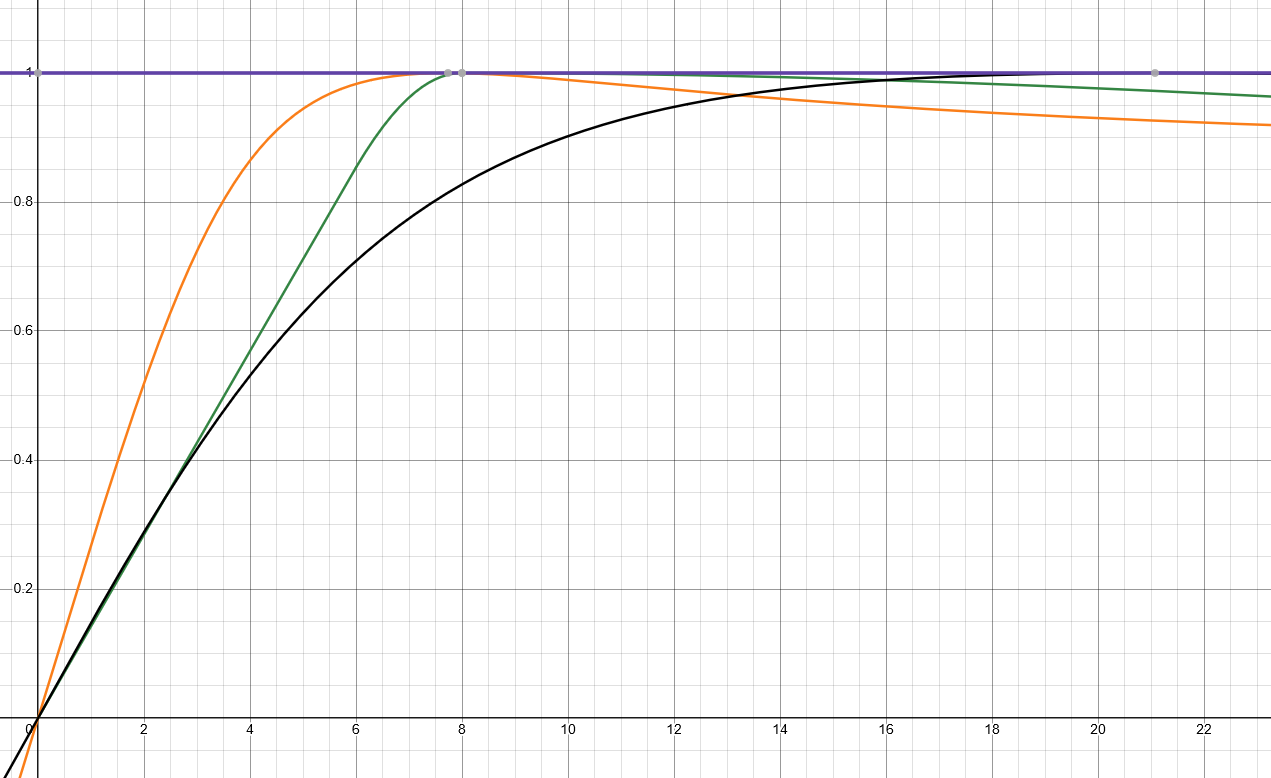
The green line is my own system. The orange line is the magic formula where the coefficient B has been adjusted to match peak slip (or close enough at least), and the black line is the magic formula where B has been adjusted to match initial cornering stiffness. Hardly scientific, I know, but from my testing you seem to have to be trying to generate a tyre that looks like mine using the Pacejka's formula. Within reasonable bounds, it's nigh-on-impossible.
I haven't done anywhere near enough testing to have any confidence in nailing down if there's a limit to how much cornering stiffness you want or the prefered rate of decay approaching peak slip angle. I don't think there's much of any relationship to any specific amount of force or any car parameters, although you can mitigate the worst of a linear setup through a well set up car and simply learning how to drive around it. If you're testing car changes, find a track to learn and get familiar with the car and how it behaves in scenarios you have a lot to compare to, but also find a way to get random pieces of road you don't recognise to avoid overfitting. I didn't appreciate how twitchy my car was until I drew a corner I'd never driven before and tried to get around it.
The question is what to do. As it turns out, the magic formula is especially good at generating very steep initial slopes. I've been banging my head against a wall looking for a function that draws a curve from a defined initial slope, smoothly to a defined peak. After you reach a slope of over 3, you get into issues where the curve peaks earlier and higher than specified. I'm looking for slopes triple that and ideally more.
Using a Bézier curve might be the best solution. They don't let you directly get an x or y value out of them, which is why I've steered clear of them, but it is technically possible to use them to generate slip curves. I've done so previously by brute forcing enough points to be able to use them as a lookup table over set intervals.
Another change, which I'll write about in depth at a later date, is to start using lateral velocity instead of slip angle to produce lateral force. Good ol' Edy's Vehicle Physics for Unity put the idea back in my head via this post when I was digging about for formulating curves, although my reasoning for doing so is entirely unrelated to theirs. The benefit of using slip velocity in my mind is that it normalises the car's response across longitudinal velocity. Call it a cowards way out, I'm tired of trying to write a decent steering filter to make all the precision of tyres work in the centimetres of analogue stick input on a gamepad. I want to make games where you fiddle with the car to make it drive how you want, not fiddle with your controller linearity to make the car manageable.




